За большинство последних достижений в области искусственного интеллекта в последние годы отвечают нейросети, от машинного перевода до компьютеров, рисующих картины, которые успешно продаются на художественных аукционах. В этом заметке мы попытаемся понять, как же работают нейронные сети.
Машинное обучение
Прежде всего, нейронные сети являются частью более широкой области, называемой Машинное обучение. Основная идея машинного обучения заключается в том, что компьютеры могут научиться выполнять определенные задачи, наблюдая за тем, как они ранее выполнялись людьми. Таким образом, нам нужны данные для обучения нейронных сетей. Например, чтобы заставить нейронную сеть отличать кошку от собаки по фотографии, нам нужно довольно много картинок картинок кошек и собак, разложенных по соответствующим папкам.
| Раздел искусственного интеллекта, изучающий то, как компьютеры могут научиться решать задачи на основе данных, называется машинным обучением. Чтобы подробнее ознакомиться с машинным обучением, рекомендую открытый курс Машинное обучение для начинающих от компании Microsoft. |  |
Нейроны: В нашем мозге и в компьютерах
Из биологии мы знаем, что наш мозг состоит из нервных клеток, каждая из которых имеет множество “входов” (аксонов) и один выход (дендрит). Аксоны и дендриты могут передавать электрические сигналы, а соединения между аксонами и дендритами обладают различной степенью проводимости (контролируемой нейромедиаторами).
| Реальный нейрон | Искусственный нейрон |
|---|
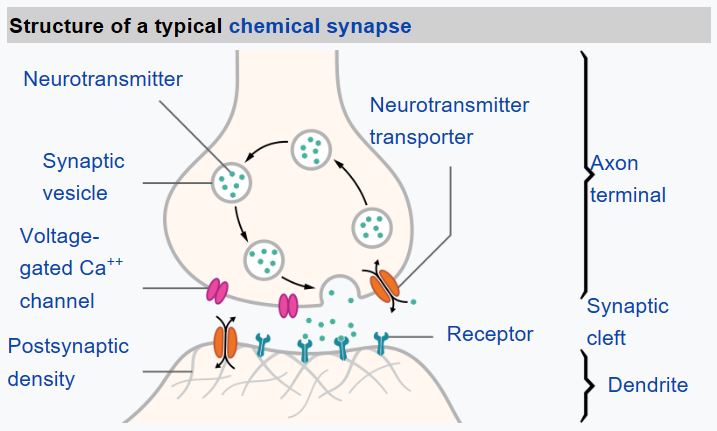 | 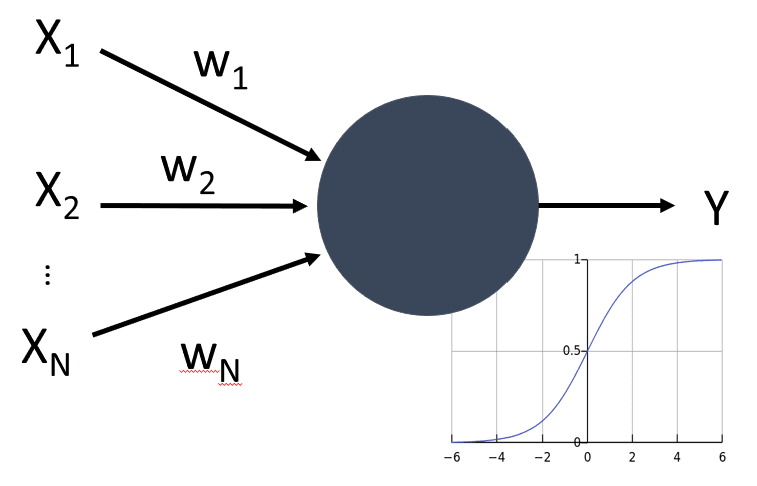 |
Таким образом, простейшая математическая модель нейрона содержит несколько входных сигналов $x_1,\dots, x_N$ и выходное значение $y$, а также ряд весовых коэффициентов $w_1,\dots, w_N$. Выходное значение вычисляется по формуле
\begin{equation} y = f\left(\sum\limits_{i=1}^N x_iw_i\right)+b \end{equation}
где $f$ - некоторая функция активации, а $b$ - некоторое число, называемое смещением.
Если мы представим веса в виде вектора $W=(w_1,\dots,w_N)$, а также запишем входные данные $X=(x_1,\dots,x_N)^T$ в векторной форме, наше уравнение можно записать как $y=WX+b$ (где $\cdot^T$ означает транспонирование).
Нейроны и тензоры
Предположим, мы хотим обучить нейронную сеть распознавать написанные от руки цифры, т.е. классифицировать входное изображение (пусть у него будет размер $28\times 28$ пикселей) на 10 различных категорий. Существует набор данных под названием MNIST, который содержит около 60000 размеченных изображений цифр, которые мы можем использовать для обучения нашей сети.
В этом случае простейшая сеть для выполнения этой задачи будет иметь $28\times28=784$ входа и 10 выходов - по одному на каждую распознаваемую цифру. По сути, она будет содержать 10 нейронов, каждый из которых отвечает за отдельную цифру. Каждый нейрон будет иметь 784 веса и одно значение смещения. Для простоты мы обычно представляем все веса в виде матрицы $784\times10$, где каждый нейрон представлен строкой. Таким образом, уравнение для нашей нейронной сети можно записать в простой матричной форме: $y=Wx+b$, где $W$ - весовая матрица, $b$ - вектор смещения, а $y$ - выходные данные сети.
При обучении нейронных сетей иногда нам приходится иметь дело с матрицами более высоких размерностей, которые называются тензорами. Например, мы часто берем несколько обучающих примеров - это называется минибатч. Минибатч из 100 изображений размером $28\times28$ может быть представлен тензором размером $100\times28\times28$.
Библиотеки для работы с нейросетями
Современные нейронные сети содержат миллионы нейронов, и состоят из большого количества слоёв - поэтому обучение нейросетей также называют глубоким обучением. Чтобы обучать такие сети, нам нужно выполнять множество матричных операций. Для ускорения такого рода вычислений удобно использовать графические процессоры (GPU), потому что все эти вычисления, по сути, легко распараллеливаются.
Чтобы упростить работу с вычислениями как на CPU, так и на GPU, существует ряд специальных библиотек или фреймворков для работы с тензорами. Наиболее популярными из них являются PyTorch и Tensorflow.
 |  |
| Один из первых фреймворков глубокого обучения, и поэтому в настоящее время он широко используется в отрасли. Он также включает упрощенный фреймворк Keras, который значительно упрощает обучение нейронных сетей. | Отличный фреймворк глубокого обучения, который быстро набирает популярность. В нем впервые было введено понятие динамического вычислительного графа |
Работа с тензорами в обоих фреймворках довольно проста:
| PyTorch | Tensorflow |
data = [[1, 2],[3, 4]]
x = torch.tensor(data)
rand = torch.rand((2,2,))
ones = torch.ones((2,2,))
zeros = torch.zeros((2,2,))
res = rand+ones*x
|
x = tf.constant([[1,2],[3,4]])
rand = tf.random.normal((2,2,))
ones = tf.ones((2,2,))
zeros = tf.zeros((2,2,))
res = rand+ones*x
|
| Подробнее | Подробнее |
Все арифметические операции выполняются поэлементно. Для умножения матриц нам нужно использовать отдельную операцию. Размеры также расширяются по мере необходимости.
Описание архитектуры сети
При работе с нейронными сетями в PyTorch или Tensorflow мы редко оперируем тензорами напрямую. Скорее, мы определяем нейронные сети как композицию слоев, где каждый слой содержит внутри себя все необходимые параметры, а также логику вычисления и обучения слоя.
Например, простейшую сеть для распознавания рукописных цифр можно определить следующим образом:
| PyTorch | Tensorflow/Keras |
model = Sequential(
Flatten(),
Linear(784,10),
Softmax())
|
model = Sequential([
Flatten(input_shape=(28,28)),
Dense(10,activation='softmax')
])
|
| Подробнее | Подробнее |
Обучение сети
Как мы обсуждали ранее, сеть для распознавания цифр получает изображение в качестве входных данных и вычисляет выходные данные, используя формулу $y=Wx+b$. Поведение сети определяется ее параметрами: $W$ и $b$. Настройка этих параметров с использованием обучающих данных называется обучением сети.
Однако, прежде чем мы начнем обучение, нам нужно пояснить несколько вещей. Обычно мы хотим, чтобы выходные данные сети представляли собой вероятность того, что на вход подана соответствующая цифра. Чтобы получить вероятности из произвольного вектора на выходе сети, мы применяем специальную функцию активации softmax.
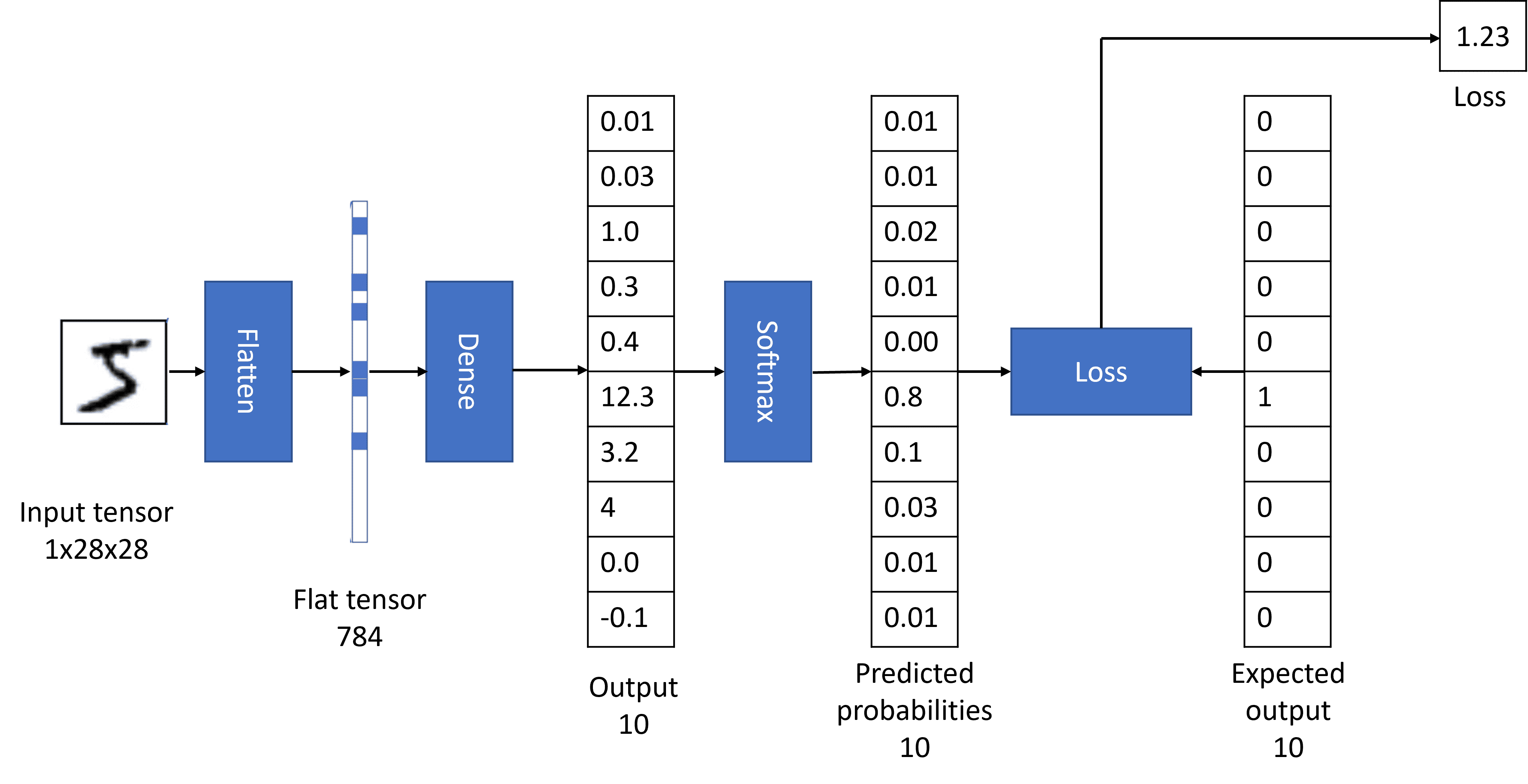
Предположим, мы подали на вход нашей сети цифру 5. Необученная сеть скорее всего даст на выходе одинаковые низкие вероятности для каждой из цифр. Однако мы хотим, чтобы выходные данные нашей сети были $(0,0,0,0,0,1,0,0,0,0)$ — вектор, представляющий число 5 (такое представление называется one-hot encoding). По тому, насколько полученный вектор вероятности похож на ожидаемое значение, мы можем рассчитать ошибку нашей сети, используя так называемую функцию потерь. В результате мы получаем число, которое говорит нам, насколько хорошо или плохо сеть работает в данный момент.
Теперь, чтобы обучить сеть, мы хотим настроить параметры $W$ и $b$ так, чтобы минимизировать эту ошибку. Для этого мы используем математическую процедуру, называемую градиентный спуск. Градиент функции показывает направление изменения параметров, при котором функция увеличивается или уменьшается наиболее быстро - таким образом, нам нужно вычислить градиент и соответствующим образом скорректировать параметры.
Все нейросетевые фреймворки позволяют автоматически вычислять градиенты. Вы можете узнать больше о том, как это делается в PyTorch или в Tensorflow.
Перед обучением нам нужно преобразовать исходные данные в тензорную форму. Часто это предполагает загрузку данных с диска и приведение всех изображений к одному размеру. Обычно все фреймворки содержат некоторые полезные функции для этого.
| PyTorch | Tensorflow |
transform = Compose([Resize(255),
CenterCrop(224),
ToTensor()])
dataset = ImageFolder('path',
transform=transform)
dataloader = DataLoader(dataset,
batch_size=32, shuffle=True)
|
dataset =
image_dateset_from_directory(
'path', batch_size=32,
shuffle=True)
|
Некоторые стандартные датасеты, такие как MNIST, могут быть загружены более простым способом, поскольку они встроены непосредственно в фреймворки для учебных целей. Например, чтобы загрузить рукописные цифры, достаточно использовать следующий код:
| PyTorch | Tensorflow/Keras |
dataset = MNIST(
root="data",
train=True,
download=True,
transform=ToTensor())
dataloader = DataLoader(
dataset, batch_size=64,
shuffle=True)
|
(x_train, y_train), (x_test, y_test) =
keras.datasets.mnist.load_data()
|
| Подробнее | Подробнее |
Обучение сети выполняется по следующему алгоритму:
- Повторяем приведенный ниже процесс обучения несколько раз, просматривая весь набор данных. Один проход по датасету называется эпохой
- Для каждой эпохи, выполняем цикл по всему набору данных, разбивая их на минибатчи. На каждом шаге мы получаем обучающие тензоры с изображениями
images и номерами классов labels. - Вычисляем выходное значение сети
out = net(images) - Вычисляем функцию потерь
l = loss(out, labels) - Используем градиент
l для подстройки параметров нейронной сети. Как правило, существует класс под названием optimizer, который осуществляет процесс оптимизации с помощью алгоритма обратного распространения ошибки. - После каждой эпохи обучения рекомендуется также посчитать точность модели на тестовом наборе данных и сохранить ее в списке, чтобы мы могли в конце построить график изменения точности в процессе обучения.
В Tensorflow/Keras весь процесс обучения реализован внутри одной функции fit. В PyTorch потребуется описать обучение более подробно:
| PyTorch | Tensorflow/Keras |
loss_fn = CrossEntropyLoss()
optimizer = SGD(model.parameters(),
lr=0.01)
for epoch in range(10):
for i, (X, y) in enumerate(dataloader):
# Compute prediction and loss
out = model(X)
loss = loss_fn(out, y)
# Backpropagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
|
model.compile(
optimizer='sgd',
loss='categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(x_train,y_train
validation_data=(x_test,y_text))
|
| Подробнее | Подробнее |
По окончании обучения, если достигнута неплохая точность, мы можем использовать нашу сеть для распознавания рукописных цифр, просто вызывая out = model(inp), где inp - тензор с входными данными. На выходе мы получим тензор вероятностей out размерности 10.
Мы можем обрабатывать несколько изображений одновременно. Например, если мы хотим классифицировать 20 различных цифр, мы загружаем их изображения в тензор размером $20\times28\times28$. В этом случае тензор out будет иметь размер 20\times10, где каждая строка содержит распределение вероятности для отдельной входной цифры. Чтобы получить фактический прогноз, мы можем вычислить номер столбца с наибольшей вероятностью, используя функцию argmax.
Выводы
Это было очень краткое введение в тему нейронных сетей, которое, тем не менее, должно дать вам достаточно информации для понимания и использования кода в PyTorch или Tensorflow/Keras. Вы можете просмотреть полный обучающий код в виде одного файла в Pytorch. То же содержимое, что и в этой статье, более подробно представлено в модулях Microsoft Learn:
Как только вы поймете основы, вы сможете перейти к более конкретным модулям про компьютерное зрение (PyTorch,Tensorflow), обработку естественного языка (PyTorch,Tensorflow)
Счастливого обучения!